Meshless Numerical Technique for Surgical Simulations

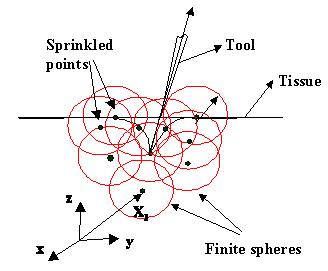
Method of Finite Spheres (MFS) is our meshless numerical scheme for laparoscopic surgical simulation that does not suffer from problems associated with meshing and remeshing. In this technique nodal points are sprinkled locally around the surgical tool tip and the interpolation is performed by functions that are nonzero only on spheres surrounding the nodes. The governing partial differential equations of elasticity are applied at the nodal points only (a technique known as “collocation”). A force extrapolation technique is then used to obtain real time performance.

Publications:

 De S, Kim J, Manivannan M, Srinivasan MA, Multimodal Simulation of Laparoscopic Heller Myotomy Using a Meshless Technique, Medicine Meets Virtual Reality:10, Newport Beach, 2002.

De, S. On the Development of an Efficient Truly Meshless Discretization Procedure in Computation Mechanics. Ph.D. diss., Dept. of Mechanical Engineering, MIT, 2001. 

De, S. and Bathe, K.J., "The method of finite spheres: a summary of recent developments," First MIT Conference on Computational Fluid and Solid Mechanics, pp. 1546-1549, Elsevier Science, 2001. 

De, S. Kim, J., and Srinivasan, M.A., "A Meshless Numerical Technique for Physically Based Real Time Medical Simulations," Medicine Meets Virtual Reality 2001 (proceedings), J.D. Westwood et al. (Eds.), IOS Press, pp. 113-118. 

De, S. Kim, J., and Srinivasan, M.A., "Virtual surgery simulation using a collocation-based method of finite spheres," First MIT Conference on Computational      Fluid and Solid Mechanics, pp. 140-141, Elsevier Science, 2001.

De, S. and Bathe, K. J., "The method of finite spheres," Computational Mechanics, 25(4): 329-345 (2000).

De S and Srinivasan MA, Rapid rendering of "tool-tissue" interactions in surgical simulations: thin walled membrane models, Proceedings of the Third PHANToM User's Group Workshop, October, 1998.